How to Find the Base of a Triangle?

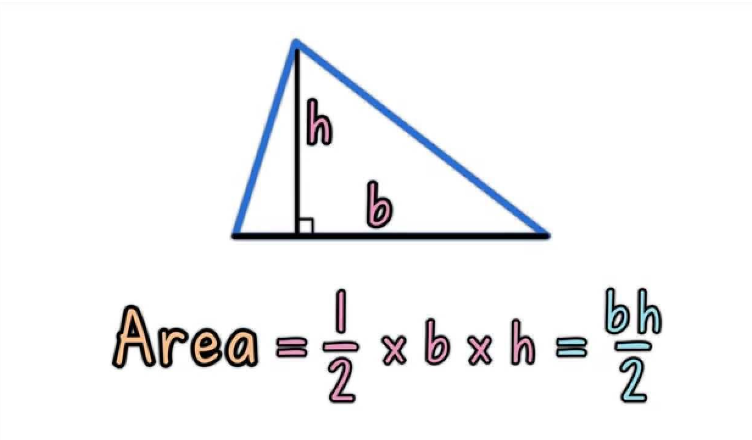
From Year 7 onwards, students in Australia start learning about triangles and their properties in maths classes. A triangle is a three-sided polygon, and the base of a triangle can be any one of its sides, usually the one which is touching the surface. The other two sides are called the height and the hypotenuse.

Our online maths tutors teach you many different ways of calculating the base of a triangle depending on the year in which you are studying and what concepts you are learning in school (for example, the area of the triangle, Pythagorean Theorem or advanced trigonometry which is part of HSC Math curriculum).

Here are some common math problem scenarios you may come across in your textbook:

How to find the base of a right-angled triangle?

A right-angled triangle is a triangle with one of its angles measuring 90 degrees. This means that the side opposite to the right angle is always the longest side or the hypotenuse. The other two sides are called the legs.

The Pythagorean Theorem states that in a right-angled triangle, the length of the hypotenuse (c) is equal to the square root of the sum of the squares of the other two sides (a and b). This means that c = √(a^2 + b^2)

This theorem is also represented using the equation:

a^2 + b^2 = c^2

So, if we are given the two sides of a right angled triangle (a and b), we can use the Pythagorean Theorem to calculate the length of the hypotenuse.

Example:

We are given that side a = 3 cm and side b = 4 cm and we have to find the base.

Using the Pythagorean Theorem, we can calculate that:

c^2 = a^2 + b^2

c^2 = 3^2 + 4^2

c^2 = 9 + 16

c^2 = 25

Therefore, c = √25

c = 5 cm

So, the hypotenuse is equal to 5 cm and side x must be equal to 4 cm (because it is the other leg of the triangle).

If we have to calculate the base of the right-angled triangle, we can use the Pythagorean Theorem to calculate the length of either side a or b.

Example:

We are given that the hypotenuse (c) is equal to 5 cm and one of the legs (x) is equal to 4 cm. We have to find the length of the other leg.

Using the Pythagorean Theorem, we can calculate that:

a^2 + b^2 = c^2

y^2 + 4^2 = 5^2

y^2 = 25 – 16

y^2 = 9

Therefore, y = √9

y = 3 cm

So, the value of y is equal to 3 cm.

How to find the base of a triangle if you know its area?

The area of a triangle is equal to half of the product of its base and height. This is represented by the formula:

Area = 1/2 x b x h

Where b is the base and h is the height.

Example:

We are given that the area of the triangle is equal to 30 cm2. We also know that the height (h) is equal to 6 cm. Now, we have to calculate its base.

To calculate the value of y, we can substitute these values into the formula for the area of a triangle:

Area = 1/2 x b x h

30 = 1/2 x b x 6

60 = b x 6

b = 10

Therefore, the value of y is equal to 10 cm.

How to calculate the base of an isosceles triangle?

An isosceles triangle is a triangle with two of its sides equal in length. The side which is different is called the base, and the other two sides are known as the legs.

If you know the value of one length of the triangle and its height, you can use the formula for the area of a triangle to calculate the value of its base.

Example:

We are given that the height (h) of the triangle is equal to 4 cm and one of the legs (L) is equal to 6 cm. We have to find the value of its base.

You can use the Pythagorean Theorem to calculate the value of the base.

a^2 + b^2 = c^2

h^2 + b^2 = L^2

16 + b^2 = 36

b^2 = 20

b = √20

b = 4.47cm

Therefore, the value of the base is equal to 4.47 cm.

Common mistakes students while calculating the base of a triangle

• In high school maths, especially when dealing with triangles, a common mistake students make is assuming that the base is always the longest side of the triangle. However, this is not always the case. The base can be any one of the three sides of the triangle and is usually denoted by the letter ‘b’.

• Another mistake students make is using the wrong formula to calculate the base. For example, if you are given the area and one side length of a triangle, you cannot use the Pythagorean Theorem to find its base. You must use the formula for the area of a triangle which is:

Area = 1/2 x b x h

Where b is the base and h is the height.

• Finally, a mistake that some students make is mixing up the letters ‘b’ and ‘h’ when using the formula for the area of a triangle. It is important to remember that ‘b’ represents the base while ‘h’ represents the height. If you mix up these letters, you will end up with the wrong answer.

The base of a triangle is an important concept in geometry and is used in a variety of calculations. In real life, the base of a triangle is often used to calculate the height of an object, such as a tree or building. It is also used in construction when measuring the dimensions of a triangular area. Knowing how to calculate the base of a triangle is a valuable skill that will be useful in many different situations.

If you are stuck on a particular question or concept, our online maths tutors can help you understand the underlying concepts so that you can solve the problem correctly. They will also provide tips and tricks to help you remember how to calculate the base of a triangle for future reference.